Cuando se estudian matemáticas en el bachillerato y en la universidad, el infinito aparece en todo su esplendor. Nos acostumbramos tanto a calcular límites cuando x tiende a infinito y a obtener límites cuyo resultado es “infinito”, que acabamos considerándolo como algo normal.
Sin embargo, el infinito es un concepto peliagudo, que nos puede llevar a paradojas que van contra la propia razón. Georg Cantor dedicó gran parte de su carrera al estudio del infinito y obtuvo resultados que van en contra del sentido común y que le acarrearon más de un enemigo y muchos disgustos personales.
El campo de estudio de George Cantor fue la teoría de conjuntos, y utilizó esta teoría para acercarse al infinito. Por ejemplo, para demostrar que los números enteros pares e impares son conjuntos con el mismo número de elementos, Cantor asignaba a cada número del conjunto de los pares, un número del conjunto de los impares:
Asignación entre los números pares e impares positivos
Si conseguimos que esta asignación sea biunívoca, es decir que a cada elemento de un conjunto le pertenezca un único elemento del otro conjunto y viceversa, habremos demostrado que ambos conjuntos tienen el mismo número de elementos. Una idea elegante y sencilla, pero veamos a dónde nos lleva esta idea si seguimos avanzando.
¿Qué os parece si ahora comparamos los números enteros con los números racionales? Los números racionales son aquellos formados por una fracción en la que numerador y denominador son números enteros. Por ejemplo, 2/1 es un número racional, que a la vez es 2, un número entero. Sin embargo 1/2 es un número racional, pero no es un número entero, ya que tiene parte decimal. Todos los números enteros pueden expresarse como un número racional, simplemente tenemos que dividirlos entre uno, pero no ocurre a la inversa.
Pero ahora comparemos ambos conjuntos a la manera de Cantor. En esta ocasión, Georg ordenó los números racionales de la siguiente forma:
En primer lugar los números cuyo numerador y denominador suman 2, luego los números cuyo numerador y denominador suman 3, y así sucesivamente, colocando primero las fracciones con un numerador menor:
Fracciones para las que la suma de denominador y numerador es 2, 3, 4 y 5.
Ahora que hemos conseguido un orden, nos bastará con ir asociando números enteros positivos a cada número racional positivo:
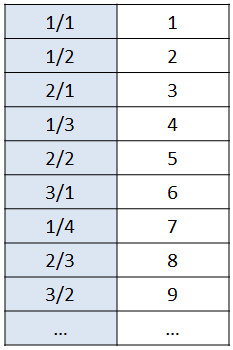Vamos situando las fracciones según la suma de denominador y numerador y vamos asignando a cada una un número entero.
Y como a cada fracción podemos asociarle un número entero y viceversa, podemos deducir que el conjunto de los números racionales tiene el mismo número de elementos que el de los números enteros.
No me miréis así, a Cantor le criticaron tanto que el hombre acabó un poco deprimido, así que ahora no os paséis conmigo, que soy un simple mensajero y queda lo mejor por contar.
Puntos, puntos y más puntos
Vamos ahora a comparar los números enteros con los números reales. Tomemos una recta cualquiera, como esta:
En esta recta hay infinitos puntos: tenemos el 0, el 1, el 0.5, el 0.5000000001, etc. Un día me preguntaron cómo representaría el concepto de infinito, pinté esta misma recta y solté una charla. Sí, tal como estáis pensando, no tengo muchos amigos.
Vamos a ver si podemos relacionar el conjunto de puntos de esta recta con los números enteros. Lo primero será buscar una forma de ordenar los puntos de la recta para poder asociarle, a cada uno, un número entero.
Veamos, podemos empezar por el cero, luego podemos coger el 0.1 y entonces mmmh… No. Si ponemos luego el 0.1 nos dejamos por el camino el 0.01, y el 0.001, y el 0.0001 y ¡UFF! ¡Podemos seguir hasta tener infinitos ceros antes de poner un miserable 1! Y bueno, estos ejemplos son números racionales, podríamos usar un truco parecido al anterior, pero es que por medio también habrá números irracionales y cada vez que queramos realizar una ordenación, el listo de turno podrá añadir un nuevo decimal y reírse de nosotros.
Cuando abrimos el tarro de las esencias de los números reales, nos aparece un número infinito de decimales y en muchas ocasiones sin ningún tipo de periodicidad.
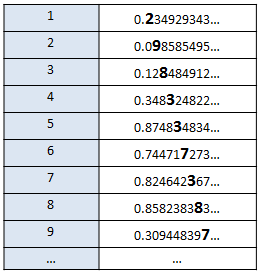
No podemos conseguir una ordenación de los puntos que hay dentro de nuestra recta que nos permita asociar cada uno de ellos a un número entero. Para realizar la demostración, Cantor pensó en un orden cualquiera asociado a los números reales entre 0 y 1, por ejemplo:
En esta matriz estarían todos los números reales entre cero y uno, con un número entero asociado. Ahora bien, formemos un número de la siguiente forma: del primer número escogemos el primer decimal, le sumamos uno y lo colocamos en el primer decimal de nuestro nuevo número; del segundo número escogemos el segundo decimal, le sumamos uno y lo situamos en el lugar del segundo decimal y así sucesivamente. En nuestro caso tendríamos: 0.309448498…
Pues bien, el número que acabamos de crear, no forma parte de la ordenación anterior. En cualquier lugar que lo coloquemos, el decimal correspondiente a esa posición será incorrecto. Por ejemplo, si lo colocáramos en la posición 9, el noveno decimal es diferente, ya que su valor es el de ese mismo decimal más uno. El número que hemos creado siempre “chocará” en la diagonal independientemente de donde queramos colocarlo. La ordenación que hemos supuesto inicialmente es imposible.
Ante este hecho, Cantor declaró que el infinito del número de puntos que se encuentran en una recta es de un orden superior al infinito del número de elementos de los números enteros.
Pero, ¿y si comparamos nuestra pequeña recta con una más grande?
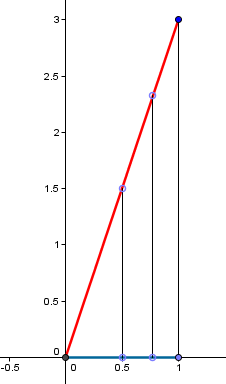
En este simple esquema, podemos ver cómo siempre podremos asignar a cada punto de la recta más grande (roja), uno de la recta más pequeña (azul). Solo hay que colocar las rectas formando un triángulo y lanzar líneas paralelas como las que vemos en el esquema.
¿Y si la segunda recta es infinitamente larga? Para verlo mejor me vais a permitir un truco: doblar la primera recta hasta formar un círculo, y lo colocamos así en nuestra recta infinita:
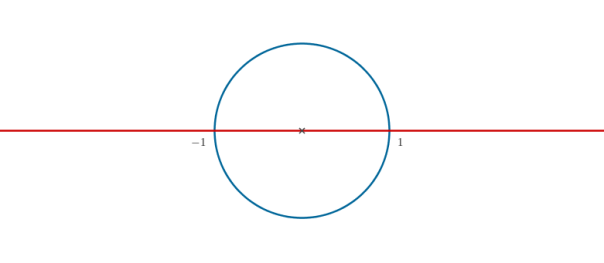Bueno, imaginad que la línea roja sigue hacia el infinito por la derecha y por la izquierda, tampoco seamos tiquismiquis.
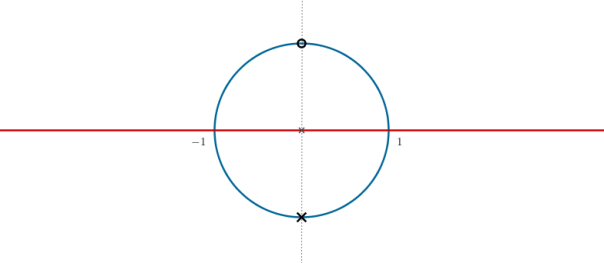
Ahora ponemos un punto fijo arriba, en la parte del círculo más alejada de la recta, y un punto móvil abajo:
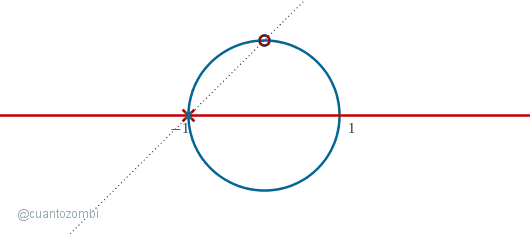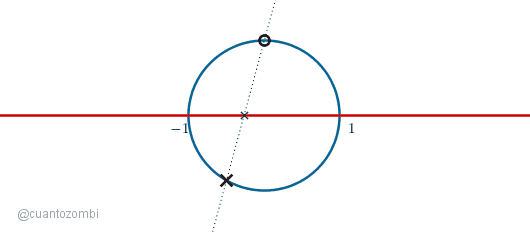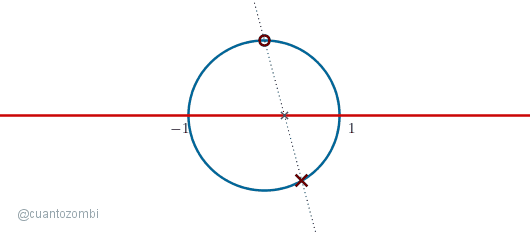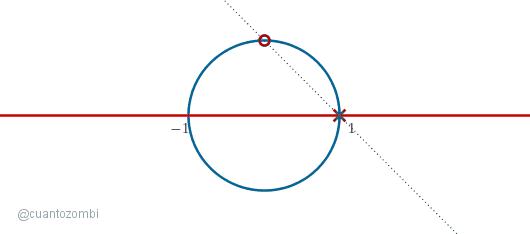
Al trazar una recta que atraviesa ambos puntos, tenemos una intersección con la línea roja. Ahora movamos el punto móvil bordeando el semicírculo que queda debajo de la línea roja:
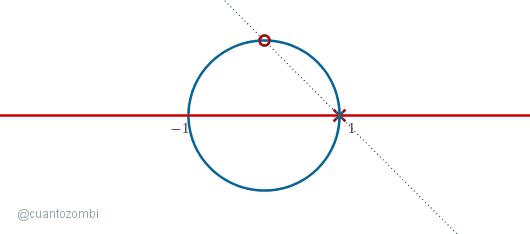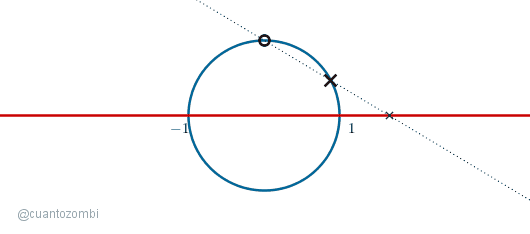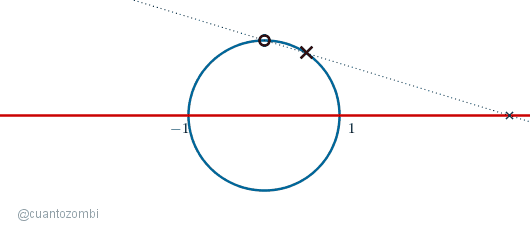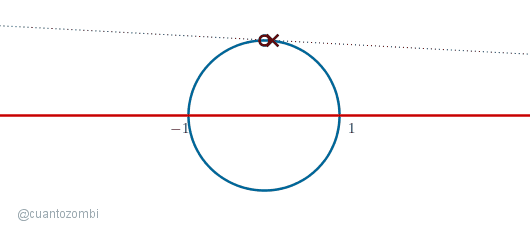
Al mover el punto sobre el semicírculo de abajo, podemos obtener cada uno de los puntos de la recta que quedan dentro del círculo. Solo tenemos que tomar pasos cada vez más pequeños si queremos más precisión. ¿Pero qué pasa cuando movemos el punto por el semicírculo que queda encima de la recta?
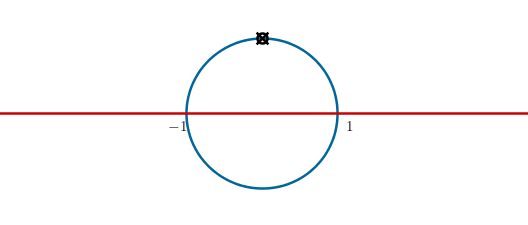
Podemos obtener todos los puntos que hay en la recta y que han quedado fuera del círculo jugando con el desplazamiento del punto móvil; a medida que lo hagamos con más precisión, podremos obtener cualquier punto que deseemos. Si queremos obtener los puntos negativos, solo tenemos que recorrer el resto del semicírculo.
Así que el conjunto de puntos de cualquier recta que elijamos tiene la misma cardinalidad, independientemente de su tamaño, incluso si tenemos una recta de un tamaño infinito.
Subiendo de dimensión
¿Y los puntos de un cuadrado? Evidentemente el conjunto de los puntos de un cuadrado tendrá un número infinito de elementos, pero ¿será comparable a una recta?
Habrá que buscar una forma de ordenar los pares de puntos de un cuadrado de forma que cada uno se corresponda con un único punto de la recta. Vamos a escoger un cuadrado de lado 1 y una recta de longitud 1:
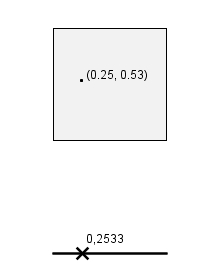
Escogemos un punto del cuadrado y obtenemos sus coordenadas, por ejemplo (0.25, 0.33). Podríamos crear a partir de estas coordenadas el siguiente número: 0.2533, incluyendo primero los decimales de la primera coordenada y luego los de la segunda.
Pero ¿y si cogemos el par de puntos (0,2 ,0,533)? Pues no, no funciona, porque el punto de la recta que obtendríamos sería 0.2533, el mismo que habíamos obtenido antes.
¿Cómo podemos conseguir una ordenación que nos permita asignar a cada par de puntos del cuadrado un punto de la recta? Piénsalo un poco, intenta dar con la forma correcta para formar el valor asignado a la recta y, cuando quieras ver la solución, ve al final del artículo.
La solución existe y llevó a Cantor a proclamar que el segundo orden de infinito era el formado por el conjunto de puntos de cualquier objeto geométrico, en un número de dimensiones cualquiera. Es decir, el conjunto de los puntos que se encuentra dentro de un cubo de cualquier tamaño tiene la misma cardinalidad que el conjunto de los puntos que hay dentro de una pequeña recta.
Hay un tercer orden de infinito descubierto por Cantor, pero esa es otra historia que merece ser contada en otra ocasión, ahora os dejo con una última paradoja.
La paradoja final
Si has llegado hasta aquí, te estoy infinitamente agradecido, aunque debo confesarte que en todo lo que he contado hay oculta una paradoja muy curiosa.
Hemos visto cómo a partir de un círculo podemos obtener todos los puntos de la recta real. ¿Todos?, ¿seguro?
A medida que acercamos el punto móvil al fijo, por la derecha o por la izquierda, obtenemos cada vez valores más grandes, prácticamente imposibles de transcribir. ¿Cuándo alcanzaremos el valor infinito exactamente? Lo lógico sería pensar que lo obtendremos cuando los dos puntos se junten, ocupando el mismo espacio.
Pero si se trata del mismo punto, ¿cómo podemos trazar la línea recta que servía para conseguir la intersección con la recta real? No, no se puede. Con un solo punto no puede definirse una línea porque, amigos, el infinito es indefinido.
MULTIPLÍCATE POR CERO
Hay una forma de llegar a formar esa línea recta, al prescindir del punto móvil y usar “otra cosa”, pero también llegaríamos a una paradoja. ¿Te animas a intentarlo?
La solución al cuadrado
Para obtener un solución al problema del cuadrado hay que utilizar un truco muy ingenioso:
Tenemos 0.25 y 0.5. Pues bien, lo que haremos será ir escogiendo en cada ocasión un decimal de cada uno de los puntos. Primero cogeremos el 2 de 0.25, luego el 5 de 0.53, a continuación el 5 de 0.25 y así sucesivamente. De esta forma tendremos:
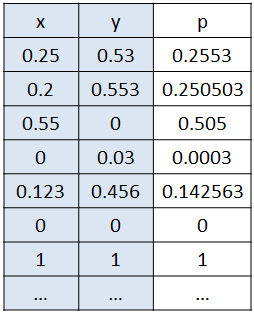Cuando una de las coordenadas no tiene el mismo número de cifras significativas que la otra, utilizaremos el cero. Por ejemplo (0.200, 0.553)
Mediante este sistema, podemos situar cada par de puntos del cuadrado en un único punto de la recta. Además, si nos fuéramos a un número mayor de dimensiones, solo tendríamos que ir repitiendo el proceso para más coordenadas, por ejemplo:
En definitiva, Cantor era un genio.
No hay comentarios:
Publicar un comentario