Lo que ven en la imagen que abre el post es un río meandroso, que no es ni más ni menos que un río de planicie, donde la pendiente es casi nula y lo que hace el río es erosionar los bordes exteriores de las curvas que genera y deposita en el lado opuesto. Esto es muy reconocido por los geólogos y sucede en TODOS los ríos del mundo.
A mediados de la década de 1990 el geólogo Hans-Henrik Stolum, de la Universidad de Cambridge , observó que la relación entre el doble de la longitud de un río y la distancia en línea recta desde su nacimiento hasta su desembocadura es, generalmente, un valor próximo a 3.
En los ríos más antiguos, que han tenido la oportunidad de desarrollar largos cursos serpenteantes, la relación se suele acercar al valor de π (3,14) y rebasarlo en los casos de meandros muy cerrados.
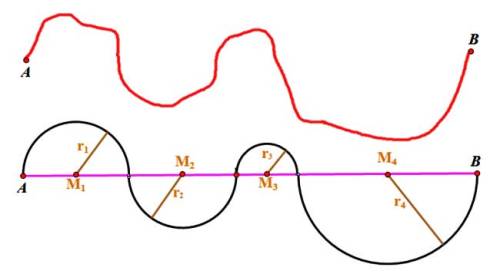
La idea es la siguiente: en la imagen puede verse el esquema del curso de un río y su ‘modelización matemática’ con semicircunferencias.
La longitud del río, de A a B, será la suma de las longitudes de las semicircunferencias
π r1 + π r2 + π r3 + π r4
y la distancia lineal entre A y B la suma de los diámetros
2 r1 + 2 r2 + 2 r3 + 2 r4
por lo que la razón entre el doble de la longitud y la distancia líneal será
2 x (π r1 + π r2 + π r3 + π r4) / (2 r1 + 2 r2 + 2 r3 + 2 r4) = π
Al físico Albert Einstein se le ocurrió la razón por la cual los ríos serpentean: cuando se forma un río se forman pequeños pliegues y dobleces en su curso y el agua que fluye en el exterior de una curva se mueve más rápido que el agua que fluye por el interior. Esto erosiona el exterior más rápidamente que el interior y el río se mueve hacia fuera, creando una curva más grande.
Con el tiempo, las curvas se cierran tanto que se encuentran y el río forma un atajo a través de ellas formando una laguna aislada… y el proceso comienza de nuevo otra vez: la relación entre el doble la longitud real del río y su longitud en línea recta tiende de nuevo a π.
Algunos de los valores de la proporción para ríos españoles son los que se presentan a continuación, calculados usando datos de Wikipedia y Google Maps:
| Río | Longitud | Distancia nacimiento-desembocadura | Proporción |
| Miño | 310 km | 189 km | 3,2804 |
| Ebro | 950 km | 507 km | 3,7475 |
| Duero | 897 km | 487 km | 3,6838 |
| Tajo | 1007 km | 649 km | 3,1032 |
| Guadiana | 818 km | 429 km | 3,8135 |
| Guadalquivir | 657 km | 336 km | 3,9107 |
Como curiosidad añadida, parece ser que la naturaleza mantiene otras relaciones en las características de un río.
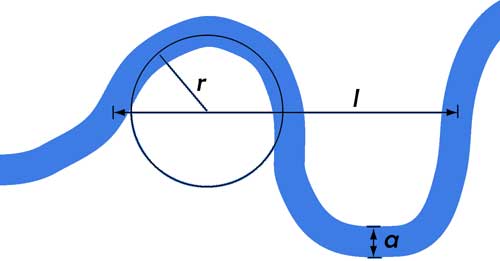
Si r es el radio de curvatura de una de las curvas del río, a es el ancho del río y les la “longitud de onda” del meandro se cumplen estas relaciones, siempre aproximadas:
r = 2,3a y l = 11a

No hay comentarios:
Publicar un comentario