Los que hayan tratado con ellos estarán de acuerdo conmigo en que cuando se enseñan por primera vez (en la SECUNDARIA normalmente) a más de uno le acarrean dolores de cabeza y confusiones. ¿Por qué tenemos que aprender logaritmos?
No me voy a meter en el eterno debate de qué es cultura y por qué es mejor saber ciertas cosas, pero si que pondré algunos ejemplos.
Usando las funciones logarítmicas
El poder de los logaritmos consiste en su utilidad para resolver ecuaciones exponenciales. Algunos ejemplos incluyen sonido (medidas de decibeles), terremotos (escala Richter), el brillo de las estrellas y química (balance de pH, una medida de acidez y alcalinidad).
Caso 1: Veamos la escala Richter, una función logarítmica que se usa para medir la magnitud de los terremotos. La magnitud de un terremoto se relaciona con cuánta energía libera. Instrumentos llamados sismógrafos detectan el movimiento de la tierra; el movimiento más pequeño que puede detectarse en un sismógrafo tiene una donde con amplitud Ao.
A – la medida de la amplitud de la onda del terremoto
Ao – la amplitud de la onda más pequeña detectable (u onda estándar)
De aquí puedes encontrar R, la medida en la escala de Richter de la magnitud del terremoto usando la fórmula:
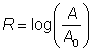
La intensidad de un terremoto típicamente se mide entre 2 y 10 en la escala de Richter. Cualquier terremoto que se registra por debajo de 5 es un terremoto menor; pueden mover un poco el suelo, pero normalmente no son lo suficientemente fuertes para causar algún daño. Los terremotos que miden entre 5 y 7.9 en la escala de Richter son mucho más severos y cualquier terremoto por encima de 8 causará mucho daño. (El grado más alto jamás registrado para un terremoto fue de 9.5, durante el terremoto de 1960 en Valdivia, Chile.)
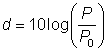
Una diferencia de 1 punto en la escala Richter corresponde a una diferencia 10 veces la amplitud en la amplitud del terremoto (que se relaciona con la fuerza de la onda). Esto significa que un terremoto que mide 3.6 en la escala de Richter tiene una amplitud 10 veces más grande que uno que mide 2.6.
Caso 2: Veamos de nuevo el ejemplo anterior. En ese ejemplo, la amplitud de onda del terremoto fue 392 veces la normal. ¿Que si hubiera sido 10 veces más o 3,920 veces la normal? Para encontrar la medida de ese tamaño de terremoto en la escala de Richter., encuentras el logaritmo de 3920. Una calculadora te da el valor de 3.5932…o 3.6, cuando lo redondeamos a décimas. ¡Un punto extra en la escala de Richter equivale a mucho más movimiento!
El sonido se mide en una escala logarítmica usando una unidad que se llama decibel. La fórmula se parece mucho a la de la escala de Richter:
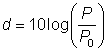
donde P es la potencia o intensidad del sonido y Po es el sonido más débil que puede captar el humano.
Caso 3: Aquí hay otro ejemplo de los logaritmos usados en contextos científicos. La medida de acidez de un líquido se llama pH del líquido. Está basada en la cantidad de iones de hidrógeno (H+) en el líquido. La fórmula del pH es:
pH = −log[H+]
donde [H+] es la concentración de iones de hidrógeno, dada en una unidad llamada mol/L (“moles por litro”; un mol es 6.022 x 10^23 moléculas o átomos).
Líquidos con pH bajo (hasta 0) son más ácidos que los que tienen un pH alto. El agua, que es neutral (ni ácida ni alcalina) tiene un pH de 7.0.
Caso 4: El brillo superficial, concepto utilizado en astronomía para describir el brillo aparente de objetos astronómicos como galaxias y nebulosas. De nuevo, matemáticamente se define por medio de logaritmos.
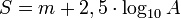
Aún así estoy muy seguro de que mucha gente piensa que esto es algo “muy forzado”, algo “que no va con ellos”. ¿Tan seguros están?
"[...] el invento de los logaritmos parece haber duplicado la vida de los astrónomos." --P.S #Laplace
#Ciencia140
— Jamessi (@jamessi_) abril 4, 2015



No hay comentarios:
Publicar un comentario